分数のわり算（前編)

「使用上の注意」

これは

算数教育では手順を教えるだけで

原理的な事は、ほったらかしにされている

分数の割り算を、私なりに解説してみようという

無謀、かつ身の程知らずな企画です。

学術的な裏付けは一切していないので

鵜呑みにしないでください。(笑)

小学校では

分数の割り算を、分数の掛け算からのアプローチで

説明していると思うのですが

ここでは

整数の割り算からのアプローチで

分数の割り算を説明してみます。

６÷２＝３

には二つの意味があります。

「１」

６個のボールを　「均等に、箱２つに分ける」　と

「１箱に入ったボールの数は３個」になる。

「２」

６個のボールを　「容量がボール２個分の箱に収める」　と

必要な　「箱の数は３つ」　になる。

「１」 方が一般的な意味だと思いますが

ここでは「２」の方を採用して説明を続けます。

次に

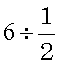
ついて考えると

６個のボールを　

「容量が（ボール半分）個分の箱に収める」

という意味になります。

「１箱の容量はボール　個分」なので

６個のボール全てを箱に収めるには

必要な　「箱の数は１２」　になります。

もし「１」の方で　　を考えると

６個のボールを「均等に、箱の数　つに分ける」

というワケの解らない意味になってしまうので

これよりは、「２」の考え方は解りやすいと思います。

今度は、分数÷分数　

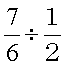
について考えます。

まず

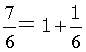　なので、これは

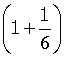個のボールを

「容量がボール　個分の箱」に収める。という意味になります。

まず、

１個分のボールを収めるため、箱が２つ要ります。

それに　個のボールは

「容量がボール　個分の箱」を　だけ埋める事ができるので

必要な「箱の数は」になります。

なので、答えはになります。

小学校で習った「後ろの分数をひっくり反して掛け算する」

方法で確認してみてください。

になるはずです。

次回はなぜ

「後ろの分数をひっくり反して掛け算する」

つまり逆数を使うと答えが出せるのか？

の解説に、挑戦してみたいと思います。

もどる